Introducción

En las últimas décadas, la formación de profesores de matemática ha sido objeto de estudio en el contexto educativo (García, 2005; León et al., 2019). Especialmente, estudiar la formación práctica de futuros profesores es un tema de interés en la disciplina (Verdugo-Hernández et al., 2024). El estudio de Sánchez (2013) muestra que la formación inicial docente (FID) ha pasado a ser un tema de políticas educativas, mientras Barbery Mourshed (2007) así como Pino-Fan et al. (2018) subrayan su importancia para el logro de la calidad de los procesos educativos en el aula. Por ello, distintas organizaciones que establecen políticas educativas han priorizado la FID en sus recomendaciones (Beech, 2004; Beech, 2007). En particular, en la formación de profesores de matemática, estas recomendaciones se centran en aspectos disciplinares y didácticos (OREALC/UNESCO Santiago, 2013).

Así pues, el estudio de la formación práctica del futuro profesor de matemática constituye un área de interés para la investigación educativa. En el estudio de Llinares (2018) se revela la necesidad de investigar en la formación docente para la comprensión de la práctica, así como los procesos de aprendizaje y desarrollo profesional de profesores de matemática que permitan la toma de decisiones en programas de formación inicial y continua.

Antecedentes de contexto: el caso de la FID en Chile

El marco legal chileno dispone de un Sistema Nacional de Aseguramiento de la Calidad de la Educación Superior (Ley 20.129 de 2006). En el caso de la formación pedagógica, esta ley establece requisitos de ingreso, define procesos evaluativos de los estudiantes y detalla indicaciones para que la Comisión Nacional de Acreditación (CNA-Chile) evalúe estas carreras. Uno de los criterios establecidos por la CNA está vinculado a la formación práctica, lo cual refiere al diseño, implementación y monitoreo de un sistema u organización formal para la formación práctica. Este eje formativo debe permitir a los futuros profesores desplegar las competencias, objetivos o resultados de aprendizaje del perfil de egreso y demostrar un desarrollo creciente de su efectividad en la docencia, en el contexto formativo (CNA-Chile, 2023).

En Chile, la FID de Matemática incorpora en universidades públicas prácticas tempranas (práctica preprofesional) como parte de la formación. Su importancia se constata en la normativa que regula la FID (Ley 20.129 de 2006; CNA-Chile, 2023), donde se considera la formación práctica como un ámbito relevante dentro de la formación. Este eje contempla diversas asignaturas de práctica preprofesional a lo largo del trayecto educativo. A modo ilustrativo, la Tabla 1 muestra su incorporación en carreras de Pedagogía en Matemática.

Estas experiencias de aula son positivamente valoradas por investigadores chilenos de reconocimiento nacional e internacional por su aporte en el campo de la formación del profesorado de matemática (Pino-Fan et al., 2018). En específico, la inserción temprana de los futuros profesores en los centros educativos ha recibido importancia estratégica, por lo cual resulta determinante que la formación práctica (profesional y preprofesional) sea investigada (Contreras et al., 2010). Otros autores muestran la relevancia de la observación de las prácticas en el proceso de formación inicial del profesorado en general (Fuertes, 2011; Arteaga-Martínez et al., 2021), de modo que permitan un análisis y reflexión sobre la acción y se transformen en herramienta de desarrollo profesional.

Instrumentos para la observación del profesor de matemáticas

La observación de clases de Matemáticas se ha ido convirtiendo en una herramienta central para el mejoramiento de los aprendizajes en las aulas, por lo que “se hace necesario el desarrollo de instrumentos que nos permitan enmarcar la observación y retroalimentación, y definir qué vamos a observar” (Martínez et al., 2018, p.40). En este sentido, distintos instrumentos han sido diseñados para la observación de profesores de matemática, entre ellos: RTOP (Evaluation Facilitation Group, 2000); IQA (Boston y Wolf, 2006); M-Scan (Berry et al., 2012); Pauta MateO (Centro de Investigación Avanzada en Educación [CIAE], 2017); Manual ProMate (CIAE et al., 2018); POEMat.ES (Joglar et al., 2021). Sin embargo, estos no se adaptan a la observación de aula en matemática en contextos de la formación práctica (Boston et al., 2015). Por su parte, Espinoza et al. (2023) dan cuenta del creciente interés en la construcción de instrumentos para la observación de la aula.

Lo anterior deja notar la relevancia de la línea de prácticas en la formación del profesorado, específicamente en educación matemática, y la escasez reportada en cuanto al diseño de instrumentos que permitan observar el desempeño en las aulas, sobre todo de los futuros profesores cuando realizan actividades formativas en contextos escolares reales. Por tanto, en este artículo se plantea como objetivo diseñar y validar un instrumento para la observación de las prácticas preprofesionales del futuro profesor de matemática.

A continuación, se presentan los fundamentos teóricos, metodológicos y empíricos que sustentan el desarrollo del instrumento. En primer lugar, se expone el marco conceptual que articula referentes normativos y teóricos desde los ámbitos pedagógico, disciplinario y didáctico-disciplinar. Posteriormente, se describe la metodología empleada para su diseño y validación, basada en juicio de expertos y análisis mediante el coeficiente V de Aiken. Los resultados se organizan en torno a las distintas etapas del proceso de construcción y evaluación del instrumento, destacando los ajustes realizados a partir de la retroalimentación cualitativa recibida. Finalmente, se discuten las implicancias del instrumento para la formación inicial docente y se plantean proyecciones para futuras investigaciones.

Fundamentación teórica

Este marco se basa en literatura especializada sobre la formación del profesorado y su conocimiento específico, abordada desde dos aristas: 1) literatura que orienta la formación inicial docente; 2) aspectos teóricos de referencia que han sido utilizados en el campo de la educación matemática para analizar el trabajo del profesorado o futuro profesor de matemática. Estas aristas se han organizado según tres ámbitos: pedagógico, disciplinario y didáctico-disciplinar (Shulman, 1986; Arteaga-Martínez et al., 2021; Van Zoest et al., 2021).

En cuanto a la revisión de la documentación y normativas vigentes en Chile, se puede indicar que los Estándares de la Profesión Docente (EPD) son el principal referente definido sobre la pedagogía que los niños, niñas y jóvenes necesitan para desarrollar su máximo potencial (Centro de Perfeccionamiento, Experimentación e Investigaciones Pedagógicas [CPEIP], 2021a). Estos estándares se proyectan en relación con dos etapas del docente: (1) su formación inicial, a través de los Estándares Pedagógicos y Disciplinarios para Carreras de Pedagogía (en adelante, Estándares FID) (CPEIP, 2021b); y (2) su ejercicio profesional, a través de los Estándares de Desempeño de la Profesión Docente, contenidos en el Marco para la Buena Enseñanza (CPEIP, 2021c). En particular, los Estándares FID (Ministerio de Educación de Chile, 2017) se plantean como pautas que explicitan y definen el conjunto de habilidades, conocimientos y disposiciones que debe tener un profesional de la educación una vez finalizada su formación inicial en los ámbitos pedagógico y disciplinario (CPEIP, 2021a).

Con respecto a aspectos disciplinares y didáctico-disciplinares, se contemplan dos modelos teóricos: 1) Conocimiento Especializado del Profesor de Matemática (MTSK por sus siglas en inglés) (Carrillo-Yañez et al., 2018), que ha sido ampliamente utilizado para analizar el conocimiento del profesorado de matemática (Martignone et al., 2022; Loría-Fernández et al., 2023); 2) Teoría de los Espacios de Trabajo Matemático (ETM) (Kuzniak et al., 2022), aplicada para analizar el trabajo matemático del profesor y de estudiantes (Henríquez-Rivas y Kuzniak, 2021). Ambas perspectivas se han manejado en complementariedad, pues permiten ahondar en aspectos didácticos y disciplinares del profesor de matemática (Espinoza-Vásquez et al., 2025; Verdugo-Hernández y Caviedes-Barrera, 2024). A continuación, se describen las dimensiones consideradas para el diseño del instrumento:

Dimensión pedagógica

El ámbito pedagógico, según CPEIP (2021b), se entiende como las competencias docentes de cualquier asignatura que aseguren interacciones pedagógicas de calidad para el logro de aprendizajes. Las mismas abarcan conocimientos, habilidades y disposiciones cuyo dominio se espera por parte de los profesores, para que sus estudiantes participen en procesos educativos.

De acuerdo con CPEIP (2021b), estas competencias se evidencian a través de prácticas que involucran al alumnado en tareas cognitivamente desafiantes, evaluación formativa y sumativa para ajustar la enseñanza y/o retroalimentar, promoción del bienestar y clima escolar positivo, explicaciones que aclaren mejor el contenido, modelamiento y uso de ejemplos, conducción de la discusión, promoción de las habilidades de pensamiento y resolución de problemas, además del uso de TIC. Estas prácticas pueden organizarse en cinco aspectos: (1) Ambiente favorable y seguro, (2) estrategias organizadas para la enseñanza, la evaluación y la retroalimentación, (3) promoción del desarrollo de habilidades a través del aprendizaje social y emocional, (4) desarrollo de las capacidades docentes y (5) apoyo a los estudiantes.

Dimensión disciplinaria

La dimensión disciplinaria se entiende, desde su conceptualización en los Estándares FID, como lo que el egresado debe demostrar en cuanto al manejo de los conocimientos propios de su disciplina (CPEIP, 2021b). Al respecto, se indica que la excelencia de la enseñanza descansa en una imbricación profunda entre el conocimiento del contenido y la capacidad pedagógica de generar representaciones, acciones y reflexiones sobre tales conocimientos (Shulman, 1986).

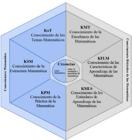
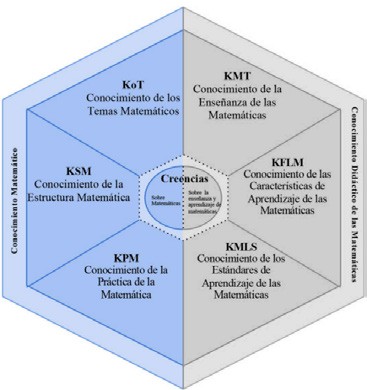
El modelo MTSK (Mathematical Teacher Special Knowledge) permite focalizar la comprensión del profesor (Carrillo-Yañez et al., 2018), siguiendo la línea de Shulman (1986) and Ball et al. (2008). Ha sido aplicado en diferentes niveles educativos (primaria, secundaria y superior), tanto con profesores en servicio como en formación (Advíncula-Clemente et al., 2020), revelando su utilidad como herramienta teórica y analítica que permite identificar el conocimiento especializado del profesor de matemática y comprender su naturaleza de manera sistemática y organizada. El modelo puede comprenderse desde dos dominios de conocimiento: conocimiento matemático y conocimiento didáctico-matemático. En la presente investigación, se procura ahondar en el conocimiento matemático (MK) que el profesor transmite y la forma en que lo despliega (Advíncula-Clemente et al., 2020). La Figura 1 muestra el modelo MTSK y la parte azul corresponde al enfoque considerado en este estudio.

El dominio MK considera tres subdominios: el Conocimiento de los Temas Matemáticos (KoT), que refiere a qué conoce y de qué manera conoce el profesor de matemáticas los tópicos que enseña, es decir, procedimientos involucrados, registros de representación, usos y aplicaciones relacionados, definiciones, propiedades y sus principios; el Conocimiento de la Estructura Matemática (KSM), que corresponde al conocimiento del profesor sobre las conexiones entre tópicos matemáticos, dentro de un mismo tema o entre temas diferentes; el Conocimiento de la Práctica Matemática (KPM), que incluye el conocimiento acerca de cómo se crea, se hace y se produce matemática, considerando reglas de construcción de un conocimiento, al igual que las demostraciones y la resolución de problemas (Advíncula-Clemente et al., 2020; Zakaryan y Soza, 2021). De este modo, el instrumento propuesto se relaciona con los referidos tres subdominios del MTSK.

Dimensión didáctica disciplinaria

El ámbito didáctico-disciplinar guarda relación con el saber específico asociado, en este caso, a la matemática y su enseñanza, involucrando el manejo del conocimiento propio de la disciplina y el conocimiento didáctico para su enseñanza. La teoría de los Espacios de Trabajo Matemático ha sido ampliamente utilizada para analizar el trabajo matemático del profesorado en el aula (Henríquez-Rivas et al., 2022; Henríquez-Rivas y Verdugo-Hernández, 2023), pues contribuye a la comprensión de qué hace el profesor al realizar tareas matemáticas y permite caracterizar los caminos que emergen en su resolución (Kuzniak et al., 2022).

En el plano epistemológico se encuentran los principios propios de los objetos matemáticos en funcionamiento, mientras que en el plano cognitivo se encuentra el pensamiento de quien usa estos objetos matemáticos para la resolución de una tarea. La articulación entre estos dos planos está dada por tres génesis: génesis semiótica, que articula el representamen, el cual considera los objetos matemáticos involucrados y los procesos de visualización, vinculados con la representación semiótica de los objetos matemáticos; génesis instrumental, que conecta artefactos, los que pueden ser materiales, tecnológicos o símbolos para el empleo de los objetos; génesis discursiva, que articula el referencial teórico y las pruebas, como todo el proceso discursivo de validación, que incluye definiciones, hipótesis, conjeturas, contraejemplos y argumentaciones deductivas (Kuzniak et al., 2016).

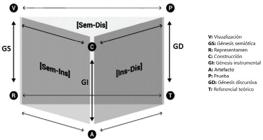
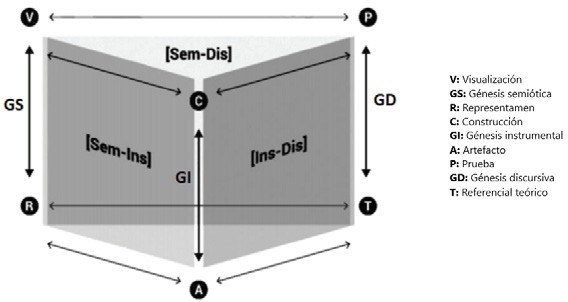
Por su parte, las distintas interacciones que se pueden dar entre dos génesis y sus componentes implicados se representan por planos verticales (Kuzniak y Richard, 2014). Estos planos verticales conectan diferentes fases del trabajo matemático y los significados en la ejecución de una tarea (Gómez-Chacón et al., 2016), lo cual se representa en la Figura 2. El plano vertical semiótico-discursivo [Sem-Dis] implica poner en coordinación el proceso de visualización de objetos representados con un razonamiento orientado hacia la comunicación matemática. Por otro lado, el plano vertical semiótico-instrumental [Sem-Ins] involucra el uso de artefactos para la construcción de resultados o exploración de objetos, mediante el uso de representaciones semióticas que permiten desarrollar una competencia ligada al descubrimiento. Por último, el plano vertical instrumental-discursivo [Ins-Dis] relaciona una prueba basada en la experimentación, la validación de una construcción o la generalización empírica, con el uso de un artefacto (Kuzniak y Richard, 2014; Kuzniak et al., 2016).

Esta investigación pone especial atención en el ETM idóneo actual del futuro profesor, entendido como el estudio del trabajo matemático que se observa y que realmente sucede en el aula durante el proceso de enseñanza de la matemática (Henríquez-Rivas et al., 2022).

Metodología

El presente estudio muestra el diseño y validación de contenido del instrumento que ha sido denominado Instrumento de observación de la práctica preprofesional del futuro profesor de matemática (IOPP-FPM). Es un estudio de enfoque mixto (Creswell y Creswell, 2023), pues en una primera etapa se realizan estudios cualitativos para la construcción del instrumento y, posteriormente, hay una etapa cuantitativa en el proceso de validación. Además, se adopta un estudio de carácter descriptivo (Lederman, 1993), pues se enfoca en realizar la construcción y evaluación de las características y propiedades psicométricas del instrumento, mediante análisis de contenido por juicio de expertos (Escobar-Pérez y Cuervo-Martínez, 2008). Para ello, se utiliza el coeficiente V de Aiken (Aiken, 1985), que permite analizar la consistencia interna del contenido de los descriptores. Este proceso contempla cinco etapas, las cuales se muestran en la Figura 3.

En la etapa 1, se realizó una revisión de la literatura, enfocada en la normativa que orienta la formación inicial docente en Chile y los aspectos teóricos de referencia que habían sido utilizados en el campo de la educación matemática para analizar el trabajo del profesorado. Estos temas se abordaron considerando ciertos referentes, entre ellos: i) desde lo pedagógico, los Estándares Pedagógicos y Disciplinarios para Carreras de Pedagogía en Matemática (CPEIP, 2021b) y el Marco para la Buena Enseñanza (CPEIP, 2021c); ii) desde lo disciplinario, el modelo MTSK (Carrillo-Yáñez et al., 2018); iii) desde lo didáctico-disciplinar, la Teoría de los ETM (Kuzniak et al., 2022).

En la etapa 2, se diseñó el instrumento de manera preliminar, de acuerdo con las categorías del marco conceptual. En la etapa 3, se realizó el proceso de validación, donde participaron siete expertos que se desempeñaban en tres universidades chilenas. Todos los informantes eran especialistas vinculados a la formación inicial y continua de profesores de matemática. Cinco de ellos eran doctores en Didáctica de la Matemática, uno de ellos era Magíster en Didáctica de la Matemática y otro era Doctor en Matemática.

A los expertos se les entregó vía correo electrónico una invitación que explicaba el contexto, la descripción y el propósito del estudio, junto con una guía para valorar los 26 descriptores iniciales, de acuerdo con su claridad (si es comprensible), pertinencia (si tiene relación con la subdimensión que mide) y relevancia (si debe ser incluido de acuerdo con el objetivo de investigación), utilizando una escala de tipo Likert para evaluar los descriptores, con puntuación de 1 a 4, que va desde el incumplimiento con la definición declarada para el criterio evaluado (1), hasta que el descriptor cumple con la definición declarada para el criterio evaluado (4). Además, se solicitó evaluar la suficiencia de los descriptores con respecto a la subdimensión correspondiente e incluir las observaciones cualitativas que permitirían mejorar los evaluados con baja puntuación. Asimismo, se incluyó un espacio para valorar aspectos cualitativos desde su perspectiva como experto.

En la etapa 4, se realizaron los ajustes, tanto al instrumento en general as a los descriptores cuyo coeficiente V de Aiken no se encontraba en un nivel aceptable, esto es, menor a 0,7 (Charter, 2003), tomando en consideración las sugerencias cualitativas recibidas. Por último, la etapa 5 contempló el diseño final del instrumento.

Resultados

Los resultados del proceso de diseño y validación del IOPP-FPM se desarrollan a continuación, expresados en las cinco etapas descritas.

Etapa 1: Revisión de la literatura

Con respecto al dominio pedagógico, se reconocieron elementos generales, que no son propiedad exclusiva de la matemática escolar como asignatura, sino que trascienden a las distintas disciplinas curriculares. En cuanto a los dominios disciplinario y didáctico-disciplinar, se reconocieron aspectos disciplinares matemáticos y actividades que evidencian el trabajo matemático del profesorado.

Etapa 2: Diseño preliminar

El diseño preliminar del IOPP-FPM se organizó en tres dimensiones: pedagógica, disciplinaria y didáctica disciplinaria. Cada dimensión se desglosó en subdimensiones y descriptores, resultando en 10 subdimensiones y 26 descriptores iniciales. La Tabla 2 presenta la estructura preliminar del instrumento.

Etapa 3: Validación de contenido

En esta etapa, siete expertos evaluaron los 26 descriptores según los criterios de claridad, pertinencia, relevancia y suficiencia. Los resultados se presentan en las Tablas 3 a 12.

Claridad

La claridad de 25 de los 26 descriptores fue evaluada muy favorablemente por parte de los expertos validadores. La Tabla 3 muestra las puntuaciones correspondientes al tercer descriptor por cada una de las dimensiones:

El descriptor 3 requiere especial atención en cuanto a claridad. Su puntuación media es la más baja de la dimensión, incluso de todo el instrumento (como se puede observar en otras tablas). Además, el coeficiente es menor al valor de corte mencionado anteriormente. Los demás muestran puntuaciones medias sobre 3 y coeficientes en niveles aceptables. En particular, los descriptores 7 y 8 obtienen puntuaciones medias máximas y coeficientes ideales.

Como se muestra en la Tabla 4, todos los descriptores asociados a esta dimensión presentan puntuaciones medias sobre 3,5 y coeficientes superiores a 0,8, por lo que, de acuerdo con los jueces, su claridad es adecuada y no necesita revisión posterior.

En esta dimensión, al igual que en la anterior, todos los descriptores muestran puntuaciones medias sobre 3 y coeficientes superiores a 0,8; particularmente el descriptor 23 alcanza puntuación y coeficiente máximo (Tabla 5). Así, la claridad de estos descriptores se determina como adecuada y no necesita revisión posterior. En general, según el criterio claridad, la revisión se concentrará en la redacción del descriptor 3, considerando la media y el coeficiente obtenido, para hacer los ajustes correspondientes de acuerdo con las sugerencias cualitativas de los jueces.

Pertinencia

La pertinencia de 25 de los 26 descriptores fue evaluada muy favorablemente por parte de los expertos consultados

Como se observa en la Tabla 6, los descriptores asociados a esta dimensión muestran puntuaciones medias mayores o iguales 3,5 y coeficientes en niveles aceptables. Los descriptores 1, 2, 5, 7 y 8 obtienen puntuaciones medias máximas y coeficientes ideales. Considerando estos datos, los descriptores no necesitan revisión posterior de acuerdo con este criterio

De acuerdo con la Tabla 7, el descriptor 17 obtiene la puntuación media más baja de la dimensión, junto con un coeficiente menor al valor crítico de aceptación definido en esta investigación. Los demás descriptores asociados a esta dimensión muestran puntuaciones medias sobre 3,5 y coeficientes superiores a 0,8, por lo que, de acuerdo con los jueces, la pertinencia de estos descriptores es adecuada y no necesitan revisión posterior

En esta dimensión, al igual que en la anterior, todos los descriptores muestran altas puntuaciones medias, sobre 3 y coeficientes superiores a 0,8. Los descriptores 20, 22, 23 y 24 alcanzan puntuación 41 media y coeficiente máximo (Tabla 8). Así, la pertinencia de estos descriptores es adecuada y, de acuerdo con los jueces, no necesita revisión posterior. Respecto al criterio pertinencia, la revisión se concentra en el descriptor 17, para hacer los ajustes correspondientes, con base en las apreciaciones cualitativas de los jueces

Relevancia

Los 26 descriptores del instrumento fueron evaluados positivamente por parte de los jueces. En efecto, este criterio es el que obtiene las puntuaciones y coeficientes más altos

En la Tabla 9 se evidencia que los descriptores asociados a esta dimensión muestran puntuaciones medias mayores o iguales 3,6 y coeficientes en niveles aceptables, mayores a 0,8. Mientras que los descriptores 1, 2, 5, 7 y 8 obtienen puntuaciones medias máximas y coeficientes ideales. Considerando estos datos, los descriptores no necesitan revisión posterior según este criterio

Los descriptores asociados a esta dimensión muestran puntuaciones medias sobre 3 y coeficientes superiores a 0,7, incluyendo los descriptores 9 y 10 con puntuaciones y coeficientes máximos, por lo cual su relevancia se califica como adecuada y no necesitan revisión posterior (Tabla 10).

Todos los descriptores asociados a esta dimensión muestran puntuaciones medias sobre 3 y 42 coeficientes superiores a 0,8. Al igual que en el criterio pertinencia, los descriptores 20, 22, 23 y 24 alcanzan puntuación media y coeficiente máximo (Tabla 11). De esta forma, la relevancia de estos descriptores resulta adecuada y no necesita revisión posterior. En relación con el criterio relevancia, no habrá revisión de los descriptores, pues las puntuaciones medias y los coeficientes están sobre el nivel definido como aceptable

Suficiencia

De acuerdo con la valoración de los jueces, los descriptores presentados son considerados suficientes para la dimensión respectiva a la que están asociados. La media y el coeficiente para el instrumento se presentan en la Tabla 12

En resumen, la revisión se concentra en los descriptores 3 y 17, de acuerdo con la valoración de los expertos y considerando sus apreciaciones cualitativas

Etapa 4: Ajustes al instrumento

Según los resultados de la validación de contenido, se puede apreciar una valoración altamente positiva al instrumento por parte de los expertos. Los criterios de claridad, pertinencia, relevancia y suficiencia obtuvieron puntajes medios cercanos al máximo y coeficientes V de Aiken en niveles aceptables. No obstante, los descriptores 3 y 17 debieron ser revisados por claridad y pertinencia, respectivamente. Además, los comentarios de 3 expertos sugirieron incorporar un espacio de valoraciones cualitativas para que el profesor supervisor tenga la posibilidad de registrar otros elementos que pudieran no estar contemplados en los descriptores mencionados.

Ajustes al descriptor 3

Las observaciones dadas por los expertos implican clarificar la redacción del descriptor: “Revisar la escritura” (Juez evaluador 4) “No queda claro lo que quiere decir” (Juez evaluador 7)

Por su parte, las sugerencias cualitativas proponen una nueva redacción del descriptor: “Puede estar en el tenor del antiguo MBE: responde de manera asertiva frente a los quiebres de las normas de convivencia” (Juez evaluador 2) “Gestiona el comportamiento de los estudiantes de acuerdo a las normas de convivencia establecidas” (Juez evaluador 3)

Los autores proponen una nueva redacción: Gestiona asertiva y efectivamente el comportamiento de los estudiantes frente a las faltas a las normas de convivencia.

Ajustes al descriptor 17

Las observaciones dadas por los expertos sugieren la eliminación del descriptor. Según señalan: “Es similar al descriptor 11. Estaría evidenciando lo mismo” (Juez evaluador 1) “Está ya fue abordado en un descriptor anterior” (Juez evaluador 2)

Por tal razón, se elimina el descriptor 17, dado que estaba incluido en otro (el 11).

Otros ajustes

Los expertos coinciden en sugerir la incorporación de un espacio de observaciones cualitativas en cada subdimensión, con el propósito de que el profesor supervisor tenga disponibilidad para dar cuenta de algún otro aspecto relevante que pudiera no estar contenido en algún descriptor.

“Sería bueno incluir un espacio asociado a las dimensiones para escribir otros aspectos emergentes” (Juez evaluador 2) “Faltaría un espacio para observaciones” (Juez evaluador 4)

Etapa 5: Versión final del instrumento

La versión final del Instrumento IOPP-FPM, luego de los ajustes relacionados con el proceso de validación y las sugerencias cualitativas de los expertos, contempla 25 descriptores organizados en dimensiones y subdimensiones. Cada uno de los descriptores está asociado a una escala de apreciación donde el profesor supervisor debe identificar si cada aspecto se observa escasamente, generalmente, frecuentemente o permanentemente en el desarrollo de la clase, o bien, si no aplica. Además, al final de cada subdimensión se incluye un espacio para observaciones cualitativas. Los descriptores por subdimensión se indican en la Tabla 13.

Discusión y conclusiones

Este artículo muestra las fases que llevan al diseño y la validación del instrumento denominado IOPP-FPM, para la observación de las prácticas del futuro profesor de matemática durante su inserción temprana, al tiempo que realza la importancia de la observación del estudiantado en sus prácticas preprofesionales, para su evaluación y retroalimentación (Fuertes, 2011; Verdugo-Hernández y Caviedes-Barrera, 2024), y la necesidad de contar con un instrumento que oriente dicha observación (Contreras et al., 2010).

La revisión que se realizó a la literatura, desde los documentos normativos en el contexto de la FID en Chile, junto con marcos teóricos que se usan frecuentemente para analizar el conocimiento y la práctica del futuro profesor de matemática, permitieron organizar el instrumento en tres dimensiones, con tres o cuatro subdimensiones cada una, cuyas definiciones teóricas permitieron la redacción de descriptores. A su vez, estos fueron validados en contenido a través del juicio de siete expertos de Matemática o Didáctica de la Matemática y las puntuaciones obtenidas fueron analizadas estadísticamente mediante el coeficiente V de Aiken. Los resultados de los juicios muestran una valoración positiva, en general, a la claridad, pertinencia, relevancia y suficiencia de estos descriptores, con algunas sugerencias cualitativas dadas por los jueces. Los resultados del análisis estadístico, junto con los ajustes hechos a partir de dichas sugerencias, permitieron proponer la versión final del IOPP-FPM, el cual se plantea como un aporte para lograr un instrumento más completo.

Con la elaboración de este instrumento se podrá obtener evidencia de las prácticas que desarrollan los futuros profesores de matemática durante su formación temprana en actividades de la práctica preprofesional. Mediante la información obtenida del IOPP-FPM es posible retroalimentar al futuro profesor y, a su vez, tomar decisiones a nivel de la formación del profesorado, con especial atención en las actividades de práctica preprofesional.

A diferencia de otros instrumentos de observación ( Evaluation Facilitation Group, 2000; Boston y Wolf, 2006; Berry et al., 2012; CIAE, 2017; CIAE et al., 2018; Joglar et al., 2021), cuyo diseño está orientado a la observación de profesores en servicio, el IOPP-FPM integra la dimensión pedagógica desde la normativa chilena vigente en relación con la FID (CPEIP, 2021b; 2021c) y las dimensiones disciplinaria y didáctica disciplinaria desde marcos teóricos (Carrillo-Yáñez et al., 2018; Kuzniak et al., 2022) que actualmente la investigación en educación matemática utiliza de forma complementaria para profundizar en la comprensión del (futuro) profesor en su formación inicial.

En cuanto a los aspectos teóricos que sustentan este estudio, una futura investigación podría considerar el subdominio didáctico-disciplinar del modelo MTSK (Carrillo-Yáñez et al., 2018) and especificidades de los ETM (Kuzniak et al., 2022), lo cual podría robustecer el instrumento y ampliar su uso en otros contextos de la formación docente. Asimismo, hallazgos del estudio de estas dos teorías en conexión podrían ser contemplados (Espinoza-Vásquez et al., 2025).

Con respecto a las limitaciones de este estudio, el número de jueces participantes como expertos en la validación de contenido pudo haber influido en los resultados obtenidos, pues a mayor cantidad de jueces evaluadores, mayor flexibilidad en el valor del coeficiente a usar (Escurra, 1988). No obstante, las características académicas de los expertos y su vínculo con la formación inicial de profesores de matemática permiten confiar en el instrumento final obtenido.

Finalmente, el instrumento diseñado y validado IOPP-FPM se pone a disposición para su uso en la observación de prácticas preprofesionales de futuros profesores de matemática durante su formación. Se proyecta que el uso de este instrumento permita aplicarlo en la formación inicial del profesorado, realizar su validación de constructo y definir perfiles o categorías del futuro profesor de matemática en el contexto de su formación práctica temprana, lo cual ayudaría a mejorar la formación del profesorado.

Disponibilidad de datos

Los datos están disponibles previa solicitud al autor correspondiente.

Referencias

Fechas de Publicación

Histórico